Kính thưa các thuật toán sort

Học lập trình trong ngành Công nghệ thông tin mà không biết Cấu trúc dữ liệu và giải thuật (CTDL & GT) tức là chưa thật sự học. Học CTDL & GT thì chắc chắn phải học các thuật toán sắp xếp cơ bản.

Trong bài viết này, mình sẽ đi sâu hơn, nhìn tổng quan hơn về bài toán sắp xếp và ý nghĩa của nó trong cuộc sống.

Tác giả: Nguyễn Trung Thành Facebook: https://www.facebook.com/thanh.it95

1. Bối cảnh

Một trong các vấn đề ta cần quan tâm đó là tìm giá trị cực đại/cực tiểu (max/min). Ví dụ: tìm bạn nữ nặng nhất lớp, xác định học sinh ngu nhất lớp, giỏi nhất lớp, v.v

Tất nhiên, khi ta chỉ có nhu cầu tìm max, min thì chỉ cần 1 vòng lặp là xong rồi. Tuy nhiên thực tế cuộc sống không chỉ như vậy. Ta thường sẽ tìm top 10 vận động viên bơi giỏi nhất, top 3 thành phố đông dân nhất, hoặc đơn giản là cần danh sách khen thưởng sinh viên dựa trên điểm học tập à danh sách cần được sắp xếp giảm dần theo điểm.

Bạn thử tưởng tượng xem, nhìn vào danh sách sinh viên theo mã số tăng dần, hoặc theo điểm trung bình giảm dần thì có dễ chịu hơn so với 1 danh sách lộn xộn, không có quy tắc nào ?

Đi sâu hơn trong ngành CNTT, ta sẽ thấy việc sắp xếp dữ liệu lại vô cùng quan trọng. Trên Facebook chẳng hạn: ta cần sắp xếp, tính toán các nội dung hiện lên news feed. Tin tức nào gần đây nhất, có liên quan đến ta nhất, thường sẽ xuất hiện ở đầu bảng tin trên Facebook. Tìm kiếm trên Google cũng vậy, ta không hề mong muốn Google gợi ý cho ta biết các loại trái cây trong khi ta đang tìm kiếm rau xanh. Kết quả nào gần với từ khóa cần tìm nhất phải được xuất hiện đầu tiên. Kết quả tìm kiếm cần được Google sắp xếp sao cho những nội dung quan trọng nhất, khớp với từ khóa nhất phải hiện lên trên cùng. Chức năng tìm kiếm bạn bè của app Zalo cũng vậy. Zalo sẽ tìm kiếm những người bạn gần với ta nhất tính theo khoảng cách địa lý, như vậy cần phải sắp xếp lại danh sách bạn bè theo khoảng cách.

Việc sắp xếp dữ liệu sẽ giúp ta tìm kiếm nhanh hơn và hỗ trợ rất nhiều cho các bài toán khác. Bài toán sắp xếp là 1 nền tảng quan trọng trong Khoa học máy tính.

Từ những nhu cầu trên, chúng ta nghiên cứu những cách thức, phương pháp để sắp xếp dữ liệu, từ đó ra đời rất nhiều thuật toán sắp xếp.

Một số thuật toán nổi tiếng, thông dụng hiện nay như: Bubble Sort, Interchange Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort.

2. Mục tiêu của bài viết này

Mình sẽ trình bày tổng quan các thuật toán sắp xếp dựa vào sự thực nghiệm. Mình sẽ không đào sâu về nền tảng lý thuyết vì những điều này đã nói rất nhiều trên sách vở, tài liệu.

Bài viết trình bày về việc test các thuật toán sắp xếp và đánh giá chúng. Ngoài ra bài viết còn nói một số khía cạnh cần quan tâm khi sử dụng thuật toán sắp xếp.

3. Điểm danh các thuật toán sắp xếp

20 thuật toán sắp xếp sẽ được lên dĩa, chưa kể mỗi thuật toán có thể bao gồm nhiều phương pháp và cấu hình ==> tổng cộng là 24 thuật toán.

Danh sách 24 thuật toán như sau

1. BlockMerge Sort
2. BST Sort (dựa trên Binary Search Tree)
3. Bubble Sort
4. Counting Sort
5. Flash Sort
6. Heap Sort
7. Insertion Sort
8. Interchange Sort
9. Intro Sort (std::sort)
10. Merge Sort (cpp std – std::stable_sort)
11. Merge Sort (top-down)
12. Merge Sort (bottom-up)
13. Noname Sort
14. Super Noname Sort --> đây là sản phẩm của mình, cải tiến dựa trên 1 ý tưởng rất hay
15. Quick Sort
16. Quick Sort (3-way)
17. Radix Exchange Sort
18. Radix Sort 4
19. Radix Sort 8
20. Radix Sort 16
21. Selection Sort
22. Shell Sort
23. Smooth Sort
24. Tim Sort

Mình sẽ test tất cả 24 thuật toán này và tìm ra quán quân vô địch.

Dữ liệu chuẩn bị:

• Source code tất cả thuật toán, mình gom lại trên 1 solution Visual Studio 2012.
• High-resolution timer.
• Chương trình sinh ra mảng input.

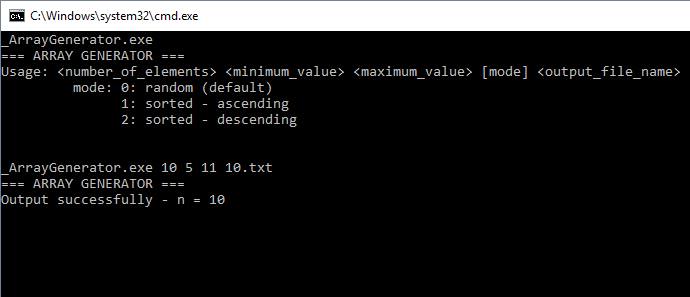
Hình minh họa: chương trình sinh ra mảng input.

Với arguments ở trên, mình đã sinh ra mảng gồm 10 phần tử ngẫu nhiên, mỗi phần tử nằm trong đoạn [5, 11]. Dữ liệu xuất ra tập tin “10.txt”.

Tất cả thuật toán sẽ trải qua 5 test cases, mỗi test case bao gồm 3 trường hợp: mảng tăng dần, mảng giảm dần và mảng ngẫu nhiên. Mỗi thuật toán đều sắp xếp tăng dần. Ngoài ra còn có 1 test case về resource.

Kết quả test là thời gian chạy của mỗi thuật toán (tính bằng nano giây). Chỉ đo thời gian xử lý, cụ thể hơn, thời gian được tính kể từ lúc sau khi input, xử lý và dừng khi xử lý xong --> output.

Ghi chú: 1 giây = 1 tỉ nano-giây.

Nào, chúng ta cùng nhau bắt đầu !

4. Test

a. Test case #1 - 10 000 phần tử

Bình thường mảng có khoảng vài chục, vài trăm phần tử là đã phê rồi. Đằng này đến 10 nghìn phần tử, có vẻ lớn ghê. Thật ra không phải như vậy, 10.000 vẫn còn quá nhỏ bé.

Với n = 10 000, mỗi phần tử nằm trong đoạn [0, 9999] thì đây là kết quả:

Theo mặc định, dữ liệu ngẫu nhiên sẽ chiếm hầu hết trường hợp, vì vậy mình ưu tiên đánh giá theo input ngẫu nhiên.

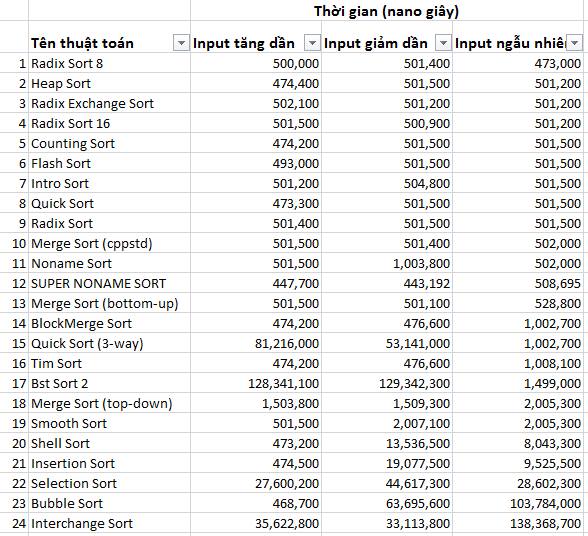
Chót bảng không ai khác ngoài 3 người anh em nổi tiếng Interchange Sort, Bubble Sort và Selection Sort. Nổi tiếng là vì nó quá thông dụng, dễ cài đặt. Tuy nhiên cái gì cũng có cái giá của nó. Nếu code cài đặt ngắn, thuật toán suy nghĩ đơn giản thì có lẽ chúng thường chỉ giải quyết các vấn đề đơn giản.

Nhưng, tất cả chỉ mới bắt đầu. 138 368 700 nano-giây ≈ 0.14 giây mà thôi. Chưa đến 1 giây nên cảm giác của chúng ta không có gì khác biệt.

Ở top 13 chạy nhanh, các thuật toán cũng không có sự khác biệt gì nhiều, do đó cũng chưa thật sự đánh giá được, mình đánh chúng đều ngang nhau.

 

b. Test case #2 - 100 000 phần tử

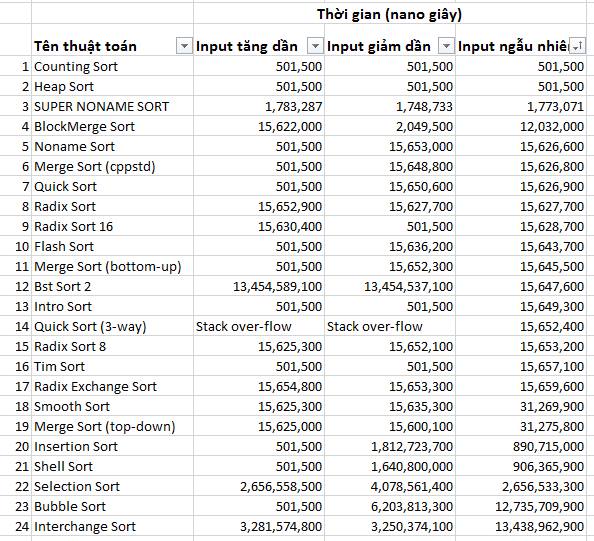
Trong lần test này, n = 100 000, mỗi phần tử nằm trong đoạn [0, 99999].

Vâng, chúng ta lại xác định được rõ top 5 chạy chậm nhất, nhìn thấy rõ luôn. Với top 17 chạy nhanh thì sự khác biệt không đáng kể. Trong top 2 có Counting Sort và Heap Sort chạy rất nhanh.

Thuật toán 3-way Quick Sort đã bị die. Khi sort thì bị lỗi. Vì build ở chế độ release nên mình không xác định được rõ lỗi gì, mình cũng làm biếng debug để biết xác định lỗi quá. Mình đoán lỗi xảy ra vì stack over-flow hoặc tràn bộ nhớ (source code em này đệ quy khá nhiều). Chiến sĩ đầu tiên của cuộc đua đã phải chia tay. Xin chia buồn !

Chúng ta cũng chia tay luôn 5 chiến sĩ chót bảng vì chạy quá chậm: Insertion Sort, Shell Sort, Selection Sort, Bubble Sort, Interchange Sort. Cần phải nhường sàn thi đấu lại cho các chiến sĩ khác tốt hơn.

c. Test case #3 – 5 000 000 phần tử

Vâng, từ 100 nghìn phần tử lên 5 triệu phần tử có vẻ hơi bị… Nhưng không sao, trong thực tế con số 5 triệu vẫn còn khá nhỏ.

Theo hiểu ngầm, giá trị mỗi phần tử nằm trong đoạn [0, 4 999 999]

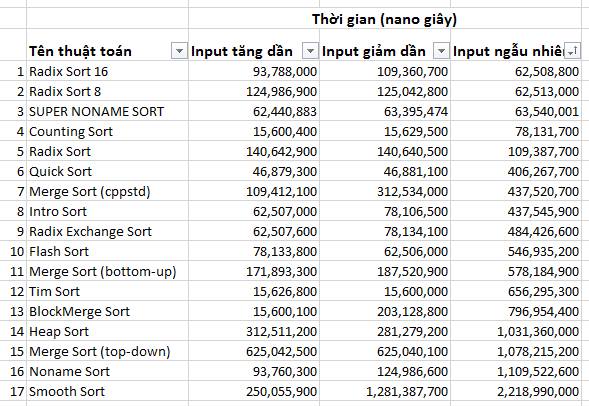
Top 3 chạy nhanh ngang nhau: 2 anh em nhà Radix Sort và 1 em Super Noname Sort. Counting Sort bám sát đằng sau.

 

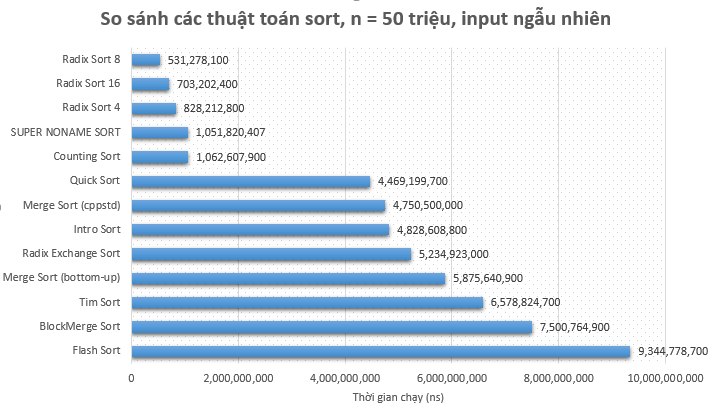
Đây là đồ thị so sánh:

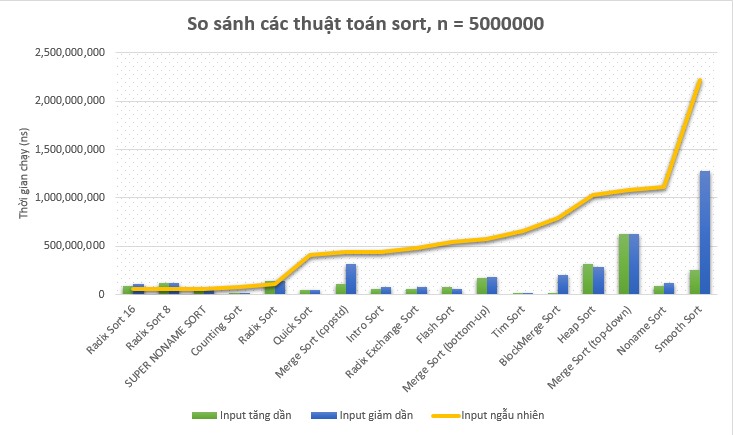
Tất nhiên, ta vẫn ưu tiên xét theo input ngẫu nhiên, với input tăng dần và giảm dần thì tỉ trọng xem xét nhỏ hơn.

Nhìn vào đồ thị trên, ta rút ra một số nhận xét:

• Một số thuật toán chạy cực nhanh khi dữ liệu đã được sắp xếp sẵn. Ví dụ: Tim Sort, Counting Sort.
• Với input giảm dần, một số thuật toán tỏ ra rất chậm chạp, ví dụ như Merge Sort (std::stable_sort), BlockMerge Sort, Smooth Sort.
• Một số thuật toán khi chạy với input ngẫu nhiên thì lại nhanh hơn so với input giảm dần/tăng dần. Ví dụ như Radix Sort, Super Noname Sort.

Trong test case lần này, không có chiến sĩ nào ra đi, tuy nhiên sang test case sau ta buộc phải chia tay với vài em.



d. Test case #4 – 20 000 000 phần tử

Từ 5 triệu lên 20 triệu, có vẻ không đơn giản. Mặc dù tỉ lệ gấp 4 lần nhưng thật ra 20 triệu là một con số không nhỏ. Nếu xét độ phức tạp thuật toán thì 5 triệu bình phương bé hơn nhiều so với 20 triệu bình phương.

 

Bảng xếp hạng trên cũng không có gì ngạc nhiên cả. Chiến sĩ Merge Sort (top-down) khá là nổi bật khi được tô chữ màu cam. Khi chạy, Merge Sort (top-down) bị crash (vì stack over-flow, hoặc tràn bộ nhớ). Mình phải build lại, test lại trên kiến trúc x64 thì Merge Sort (top-down) không còn lỗi.

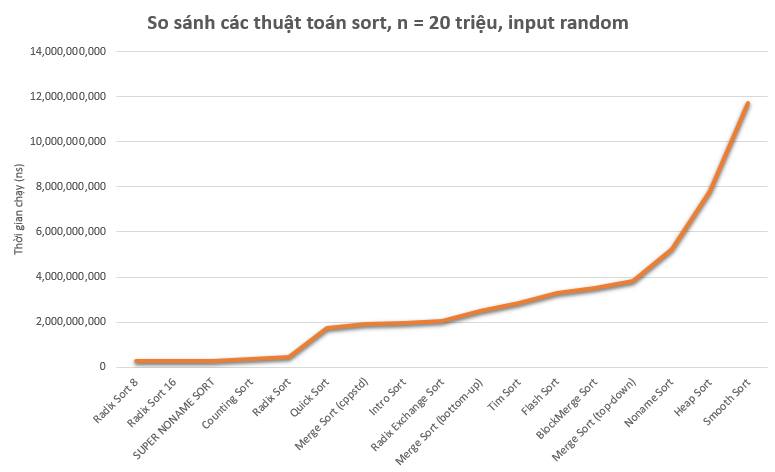
Top chạy nhanh: anh em nhà Radix Sort, Super Noname Sort, Counting Sort.

Top chạy khá nhanh: Quick Sort, Merge Sort (std::stable_sort), Intro Sort (std::sort).

 

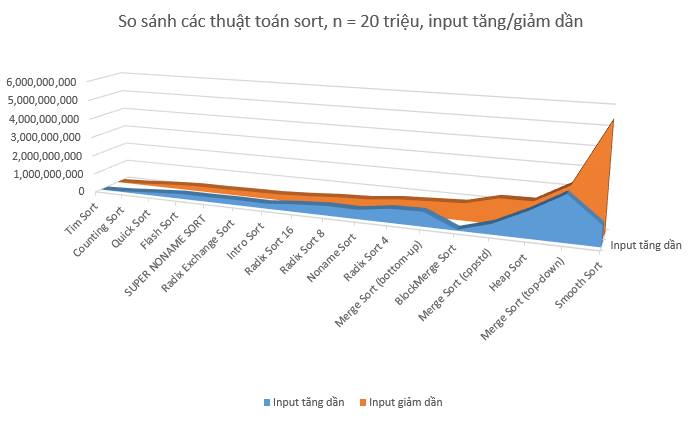
Như đã nói ở test case trước, thuật toán chạy nhanh nhất khi dữ liệu đã được sắp xếp đó chính là Tim Sort. Có một điều khá thú vị là BlockMerge Sort và Smooth Sort khi input đã sắp xếp tăng dần thì thời gian rất thấp nhưng khi input sắp xếp giảm dần thì…

Chúng ta cùng nhau nói lời chia tay với top 4 chót bảng input random, bao gồm Merge Sort (top-down), Noname Sort, Heap Sort và Smooth Sort.

Heap Sort, mặc dù được đánh giá là thuật toán có độ phức tạp ổn định O(nlogn) so với Quick Sort, tuy nhiên trong thực tế Heap Sort chạy chậm hơn Quick Sort nhiều.

 

e. Test case #5 – 100 000 000 phần tử

Vâng, 100 triệu phần tử, một con số không hề nhỏ, đủ để gây khó khăn bất cứ thuật toán sort nào. Đây là bộ test quyết định thuật toán nào sẽ thật sự dành chiến thắng.

Bạn đoán ai sẽ dành chiến thắng ?

Với 100 triệu phần tử số nguyên dương, file input có dung lượng….gần 1GB.

 

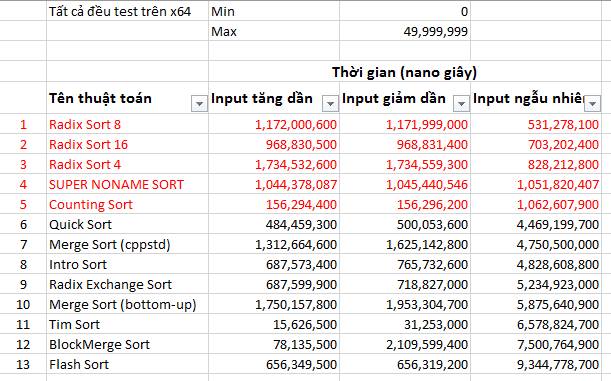
1. Quán quân: Super Noname Sort với thời gian vượt trội so với tất cả đối thủ.
2. Á quân: anh em nhà Radix Sort.
3. Quý quân: Counting Sort.

 

Ghi chú: thuật toán Super Noname Sort có thời gian chạy 162 489 416 nano giây, đây là thời gian tính từ lúc sau khi input đến khi xử lý xong ra kết quả. Nếu thật sự tính thời gian sắp xếp của Super Noname Sort thì bạn cứ lấy thời gian trên chia cho 4 --> thời gian sort là khoảng 40 triệu ns. Với bộ test 20 triệu phần tử thì thời gian sort còn nhỏ hơn nhiều nữa.

 

Nhìn chung, đây là phần test tổng quan thực nghiệm, bạn có thể test chi tiết hơn đến mức độ đếm số phép so sánh, số phép hoán vị, v.v

 

a. Test case #6 – test resource với 100 000 000 phần tử

Ta sẽ xem xét các thuật toán sort ngốn bao nhiêu tài nguyên.

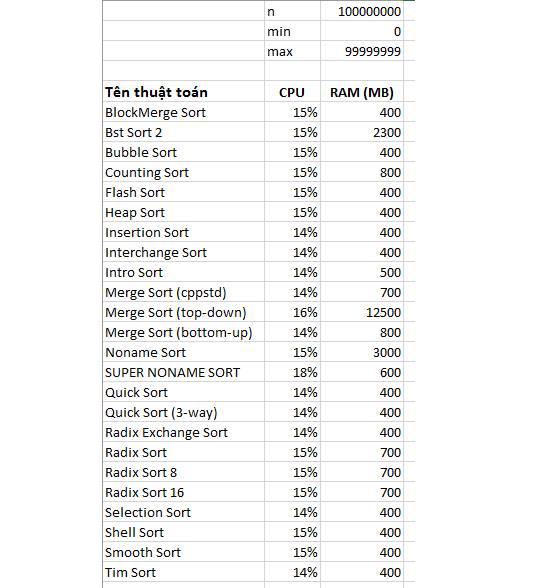
Thuật toán Merge Sort thông dụng thường là dạng top-down ==> chiếm bộ nhớ nhiều khủng khiếp khi ngốn đến 12500 MB = 12.5 GB RAM, wooooooow.

Tiếp đến là Bst Sort. Dễ dàng nhận thấy ta xử lý trên cây nhị phân, cho nên phải tốn nhiều bộ nhớ cho các node. Dung lượng RAM mà Bst Sort chiếm là khoảng 2.3 GB.

Cuối cùng là Noname Sort. Thuật toán này được bảo đảm chạy với tốc độ O(n log log n) cho trường hợp xấu nhất. Nó sử dụng danh sách liên kết nên việc ăn nhiều RAM cũng không phải là điều khó hiểu.

Nếu xét riêng về CPU thì không có sự khác nhau nhiều giữa các thuật toán.

 

5. Một số yếu tố cần quan tâm khi sử dụng thuật toán sort

Theo thí nghiệm ở trên, liệu ta sẽ sử dụng các thuật toán sort nằm trong top ?

Câu trả lời là: không.

Những lập trình viên kì cựu không bao giờ áp dụng 1 thuật toán sort cho tất cả mọi bài toán. Tùy vào bài toán với bối cảnh cụ thể, với giới hạn về thời gian, tài nguyên và đặc điểm dữ liệu mà ta có thể áp dụng các thuật toán sort khác nhau. Sau đây là một số yếu tố ta cần quan tâm.

a. Độ phức tạp thuật toán

Đây là yếu tố chính khi đánh giá thuật toán sort. Độ phức tạp thuật toán có thể hiểu là tổng khối lượng công việc mà thuật toán sẽ xử lý. Nếu độ phức tạp nhỏ ==> khối lượng công việc nhỏ ==> thời gian chạy nhanh hơn.

Độ phức tạp thuật toán chủ yếu được đánh giá bởi 3 thành phần là độ lớn dữ liệu (n), số phép so sánh và số phép gán.

Ví dụ, xét thuật toán Interchange Sort:

Ta nhận thấy có 2 vòng lặp for chạy xuyên suốt mảng.

• Với i = 0 thì vòng lặp for j lặp lại (n – 1) lần.
• Với i = 1 thì vòng lặp for j lặp lại (n – 2) lần.
• Với i = 2 thì vòng lặp for j lặp lại (n – 3) lần.
• …
• Với i = n-1 thì vòng lặp for j lặp lại (n – n) lần.

 

Như vậy, tổng số lần lặp là P = (n – 1) + (n – 2) + … + (n – (n – 1)) = 1 + 2 + 3 + … + n

==> P = 0.5 n (n + 1). Theo quy nạp Toán học thì P ≈ n^2.

Mặc dù có thể hơi khó hiểu, nhưng nếu ta nhìn tổng quan: 2 vòng lặp for lồng nhau, mỗi vòng lặp lặp lại khoảng n lần ==> n^2 lần ==> độ phức tạp là O(n^2).

 

Một thuật toán có độ phức tạp trung bình là O(n^2) thì được đánh giá là chưa tốt, thời gian chạy rất lâu. Tuy nhiên những thuật toán loại này thì đa số rất dễ cài đặt, và rất thông dụng như: Bubble Sort, Interchange Sort, Insertion Sort, Selection Sort.

Lời khuyên: đối với những bài toán đơn giản như: sắp xếp danh sách 1000 học sinh theo điểm trung bình, sử dụng 1 trong những thuật toán trên là quá đủ rồi. Vừa đơn giản vừa dễ cài đặt. Bạn không nhất thiết phải sử dụng các thuật toán top chạy nhanh vì hầu hết chúng rất phức tạp, cài đặt dễ sai.

 

Các thuật toán tốt và chay nhanh hiện nay thường có độ phức tạp là O(nlogn).

 

b. Số phép gán

Mặc dù phần b này cũng thuộc phần a ở trên, nhưng mình tách riêng vì một số lý do nhất định.

Xét một tình huống cụ thể đối với loại dữ liệu tổ hợp (ví dụ như struct/record). Ta có struct HocSinh với rất nhiều thông tin bên trong, dữ liệu của 1 học sinh là khá lớn. Ta cần sắp xếp danh sách học sinh theo điểm trung bình. Số lượng học sinh (n) là rất lớn.

Với 1 thuật toán mà số lần hoán đổi giá trị là cao, liệu có phù hợp cho bài toán trên hay không ? Khi ta hoán đổi giá trị 2 học sinh trong mảng, chương trình phải ngầm hoán đổi họ tên, CMND, mã số, địa chỉ nhà, danh sách môn học,…sẽ tốn rất nhiều chi phí. Cho dù là thuật toán top chạy nhanh đi nữa mà hoán đổi quá nhiều thì cũng có thể chạy chậm trong bài toán này.

 

c. Tính ổn định (stable)

Khi có 2 giá trị a và b trong mảng bằng nhau, ta sẽ có 2 cách sắp xếp mảng: a nằm trước b và a nằm sau b. Giá trị chúng bằng nhau ==> ta không cần quan tâm a trước b hay b trước a ???

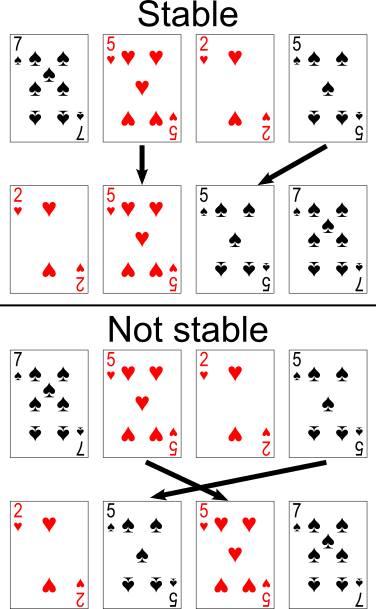
Hình từ Wikipedia.

Thuật toán được gọi là stable nếu vị trí tương đối giữa a và b không thay đổi sau khi sắp xếp. Ví dụ như hình trên, ta có 5 đỏ nằm phía trước 5 đen. Nếu thuật toán sort sau khi xử lý mà 5 đỏ vẫn nằm trước 5 đen thì đó là stable (và ngược lại, nếu 5 đỏ nằm sau 5 đen, bị ngược chiều ==> không stable).

 

Lấy lại bối cảnh như bài toán sắp xếp danh sách học sinh ở trên, giả sử ta sắp xếp danh sách theo điểm trung bình giảm dần. OK mọi thứ vẫn tốt đẹp dù là stable hay unstable.

Tuy nhiên, nếu ta đổi lại đề bài: sắp xếp theo điểm trung bình giảm dần. Nếu điểm trung bình bằng nhau thì ưu tiên sắp xếp theo học lực giảm dần. Có vẻ gặp vấn đề rồi đây.

Nếu là thuật toán không stable, ban đầu ta sắp xếp theo điểm trung bình. Có thể cùng điểm trung bình nhưng học lực kém lại phía trên học lực giỏi (và ngược lại). Kết quả của ta là danh sách A. Từ danh sách A ta tiếp tục sắp xếp theo điểm trung bình sẽ được danh sách B. Chắc gì thứ hạng sẽ được bảo toàn ?

Với thuật toán stable thì khác. Ban đầu ta cho thuật toán stable sắp xếp theo điểm trung bình được danh sách A. Từ danh sách A tiếp tục sắp xếp theo học lực được danh sách B. Vì danh sách A được bảo toàn theo điểm trung bình, cho nên khi sắp xếp danh sách A theo học lực ta sẽ bảo toàn được thứ hạng trước đó.

Nói tóm lại, tính stable cũng rất quan trọng, nó hỗ trợ ta chuẩn bị cho các công việc tiếp theo. Ví dụ trong Excel ta thường thống kê top 10 theo tiêu chí A, nếu giá trị A bằng nhau thì ưu tiên xếp hạng theo tiêu chí B, nếu giá trị B bằng nhau thì ưu tiên xếp hạng theo tiêu chí C, v.v

 

d. Tài nguyên sử dụng

Các số thuật toán cần sử dụng các biến tạm để hỗ trợ, cần sử dụng thêm RAM, phần cứng khác… Chúng đều được xem là tài nguyên sử dụng.

Các thuật toán thường có nguyên tắc đánh đổi: nếu tài nguyên sử dụng nhiều thì thuật toán chạy nhanh, và ngược lại.

Các thuật toán thông dụng như Bubble Sort, Interchange Sort, Selection Sort,… thường sử dụng tài nguyên cực nhỏ (1, 2 hoặc 3 biến tạm….).

Thuật toán Super Noname Sort top 1 của mình ở trên, mặc dù là top nhưng thật ra nó không hữu ích khi chạy bình thường. Chỉ khi nào cần tính toán dữ liệu lớn; CPU, GPU, RAM đủ mạnh thì nó mới phát huy tác dụng tối đa. Nó cũng kén chọn phần cứng, không phải máy tính nào cũng chạy được Super Noname Sort. Bật mí: Super Noname Sort sử dụng khá nhiều bộ nhớ.

 

e. Tính tổng quát

Một số thuật toán chỉ chạy được trên số nguyên ==> không tổng quát. Tuy nhiên những tên tuổi nổi cộm trong danh sách này lại đứng top, ví dụ như Counting Sort, Radix Sort.

Xoay sở: Radix Sort vẫn có thể chạy được trên số thực, nhờ vào sắp xếp từng phần dựa trên chuẩn IEEE 754 về số chấm động.

 

f. Tính in-place

Tính in-place là việc thuật toán có thể sắp xếp ngay trên dữ liệu input. Một số thuật toán phải xuất kết quả ra mảng khác (mảng input vẫn giữ nguyên ban đầu), ví dụ như Radix Sort, Counting Sort. Bạn nghĩ xem nếu mỗi phần tử là 1 struct rất lớn, thì việc ghi dữ liệu output ra mảng khác sẽ mất nhiều chi phí hay không ? In-place thường có lợi hơn nhưng đôi khi phải đánh đổi bằng tính unstable.

 

6. Phụ lục

a. Bảng tổng hợp thông tin các thuật toán sort

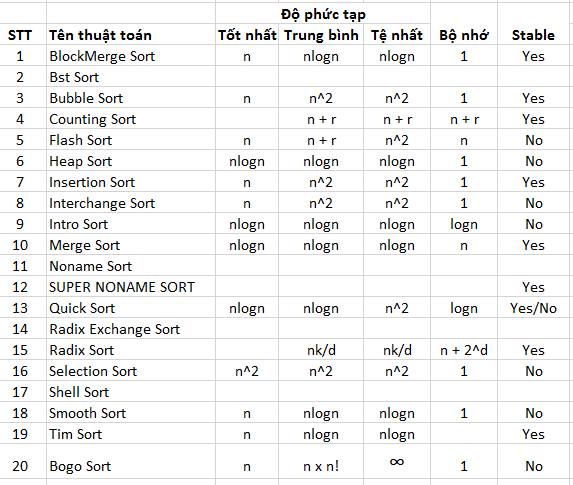
(Theo Wikipedia).

 

b. Giới thiệu sơ lược các thuật toán sort

1. Bubble Sort: dựa trên nguyên tắc “nổi bong bóng trên mặt nước”. Bong bóng nào nhẹ nhất sẽ nổi lên trên. Mỗi phần tử trong mảng như 1 bong bóng, phần tử nào nhỏ nhất sẽ dần dần được đẩy về đầu mảng.

2. Interchange Sort: dựa trên quy tắc: từ vị trí (i + 1) đến cuối mảng, ta chọn phần tử nhỏ nhất để đưa vào a[i]. Ví dụ: ban đầu ta đưa phần tử nhỏ nhất về a[0], tức là tại i = 0, ta tìm kiếm từ a[1] đến cuối mảng xem phần tử nào nhỏ nhất, và đưa nó về a[0]. Sau đó tại i = 1, ta tìm kiếm từ a[2] đến cuối mảng xem phần tử nào nhỏ nhất và đưa về a[1]. Nhỏ nhất từ a[2] đến cuối mảng tức là nhỏ thứ nhì trong toàn mảng.

3. Insertion Sort: giả sử ban đầu ta đã có 1 mảng đã sắp xếp. Như vậy khi ta đưa 1 phần tử mới vào mảng này, ta dễ dàng xác định được vị trí chèn vào (dùng 1 vòng lặp for để tìm kiếm), sau đó chèn vào. Từ 1 mảng input ban đầu, ta “chèn từ từ” các phần tử vào mảng output.

4. Quick Sort: Hoarec (tác giả) đã rất mạnh dạn khi ông đặt tên thuật toán của mình là Quick Sort (sắp xếp nhanh), và quả thật đây là thuật toán sắp xếp rất nhanh. Lấy ý tưởng từ việc đặt 1 cái chốt, cái chốt này sẽ chia mảng làm đôi. Tất cả phần tử nhỏ hơn cái chốt sẽ đưa về bên trái cái chốt, tất cả phần tử nào lớn hơn cái chốt sẽ đưa về bên phải. Cứ thế lặp lại mãi đến khi mảng con chỉ còn 1 phần tử.

5. Heap Sort: dựa trên quy tắc vun đống heap. Cái này khá phức tạp nên mình không diễn đạt = chữ ở đây được.

6. Merge Sort: ban đầu ta cưa đôi mảng thành 2 phần A và B. Ta sắp xếp toàn bộ mảng con A, sắp xếp toàn bộ mảng con B. Sau đó ta gộp A và B lại rất dễ dàng để được 1 mảng được sắp xếp.

7. Radix Sort: sắp xếp dựa trên cơ số. Nếu nói chính xác thì sẽ khá dài dòng. Ở đây bạn tạm hiểu ta có thể sắp xếp theo hàng đơn vị trước, sau đó đến hàng chục, hàng trăm,…

8. Couting Sort: đây là 1 thuật toán cụ thể của thuật toán tổng quát hơn: Bucket Sort. Để cho dễ hiểu, mình sẽ nói đơn giản: thuật toán này dựa trên việc thống kê tần suất xuất hiện các phần tử. Counting Sort thì nhanh thật đấy, nhưng còn tùy vào miền giá trị của mỗi phần tử.

9. Super Noname Sort: đây là 1 cái tên khá bí ẩn. Thuật toán này khác với tất cả thuật toán còn lại nhờ việc tận dụng phần cứng máy tính. Bạn có thể hiểu như việc ta chia mảng input thành 4 phần, mỗi phần ta nhờ 1 thread của máy tính xử lý đồng thời, sau đó gộp lại thành mảng output. Nói thêm: thuật toán này chỉ là sự cải tiến, tối ưu của mình dựa trên các ý tưởng đã có sẵn chứ không có gì ghê gớm cả ^^.

10. Bogo Sort: không nằm trong danh sách test nhưng mình đưa vào giới thiệu. Đây có lẽ là thuật toán thú vị nhất: sắp xếp dựa trên sự may mắn. Từ mảng input, ta ngẫu nhiên hoán đổi xáo trộn ngẫu nhiên các phần tử. Nếu kết quả là mảng đã sắp xếp thì coi như xong, còn nếu không thì….cứ lặp lại tiếp. Nếu may mắn, chỉ trong 1 lần xáo trộn duy nhất là ta được mảng đã sắp xếp. Tuy nhiên tỉ lệ may mắn cực kì thấp. Vì vậy Bogo Sort có độ phức tạp là O(vô cực), thật hài hước ! Tuy nhiên đừng vội cười, với các máy tính lượng tử trong tương lai, ta có thể chạy Bogo Sort với thời gian siêu nhanh, thậm chí nhanh nhất có thể.

Các bạn có thể Google để kiếm mã nguồn các thuật toán này và tự thử nghiệm, vui lòng đừng nhắn tin xin code của mình nhé.

Trên đây mình chỉ điểm danh một vài thuật toán. Trong thực tế còn rất nhiều, bạn có thể tự nghiên cứu.

 

c. Cấu hình test thử nghiệm

Đây là cấu hình mà mình test các thuật toán ở trên.

• CPU: Intel Xeon E3-1230 v5 3.4 GHz Skylake.
• RAM: 16 GB DDR4 bus 2666.
• VGA: nVIDIA GTX 1050 Ti.
• Hệ điều hành Windows 10 Professional v1607.
• Compiler: Visual C++ 2012/2015.

Khi bạn tự test, chưa chắc kết quả đã giống mình vì sự khác nhau về cấu hình và nhiều yếu tố khác. Tuy nhiên mình nghĩ rằng kết quả cuối cùng sẽ không có sự khác biệt nhiều.

 

7. Lời khuyên cho những bạn mới học lập trình và giải thuật

Bạn không cần phải học hết tất cả các thuật toán sort. Bạn chỉ cần nắm vững tư tưởng của nó, học thuộc vài thuật toán thông dụng như Interchagne Sort, Bubble Sort, Selection Sort. Sau đó khi học nâng cao hơn thì bạn có thể học Quick Sort, Merge Sort.

Bạn cũng nên tìm hiểu thư viện chuẩn (kèm theo mỗi ngôn ngữ lập trình), đa số sẽ hỗ trợ các hàm sort cho bạn.

 

8. Một số nguồn tham khảo

Một số nguồn mà bạn nên vào tham khảo nếu cảm thấy thích:

Wikipedia: https://en.wikipedia.org/wiki/Sorti...

Video demo các thuật toán sort kèm theo âm thanh sinh động: https://www.youtube.com/watch?v=kPR...

 

9. Kết luận

Không phải thuật toán sort nào tốt là sử dụng, phải là tốt trong hoàn cảnh cụ thể. Nếu nhu cầu của ta là bình thường thì hãy áp dụng các thuật toán sort cơ bản là đủ.

Xét cho cùng, cần tính toán nhanh ta cứ sử dụng Quick Sort (theo bộ test của mình, Quick Sort nằm trong top chạy khá nhanh).

Và cuối cùng, mình xin cảm ơn những nhà Khoa học máy tính đã sáng chế ra các thuật toán sort này, nó giúp mình rèn luyện tư duy nhiều hơn và khám phá nhiều điều thú vị hơn.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Tác giả bài viết: Nguyễn Trung Thành – Đại học Khoa học Tự nhiên TP HCM.

Facebook: https://www.facebook.com/thanh.it95

Hầu hết mọi hình ảnh, dữ liệu trong bài viết này đều từ Nguyễn Trung Thành. Vui lòng hỏi ý kiến tác giả trước khi sao chép.

Nguồn: FB